1. The Big Picture

Perspectives

Primary goal for programmers is to create code that is functional and easy to understand.
While ensuring good performance is important, it is crucial not to over-prioritize it.
Overemphasizing performance can result in unnecessarily complex code, making it hard to manage.

Big-O Notation

Big-O notation is a generalized metric used to describe the upper bound of an algorithm's runtime or space complexity, expressing how an algorithm's performance scales as input size increases.
Definition

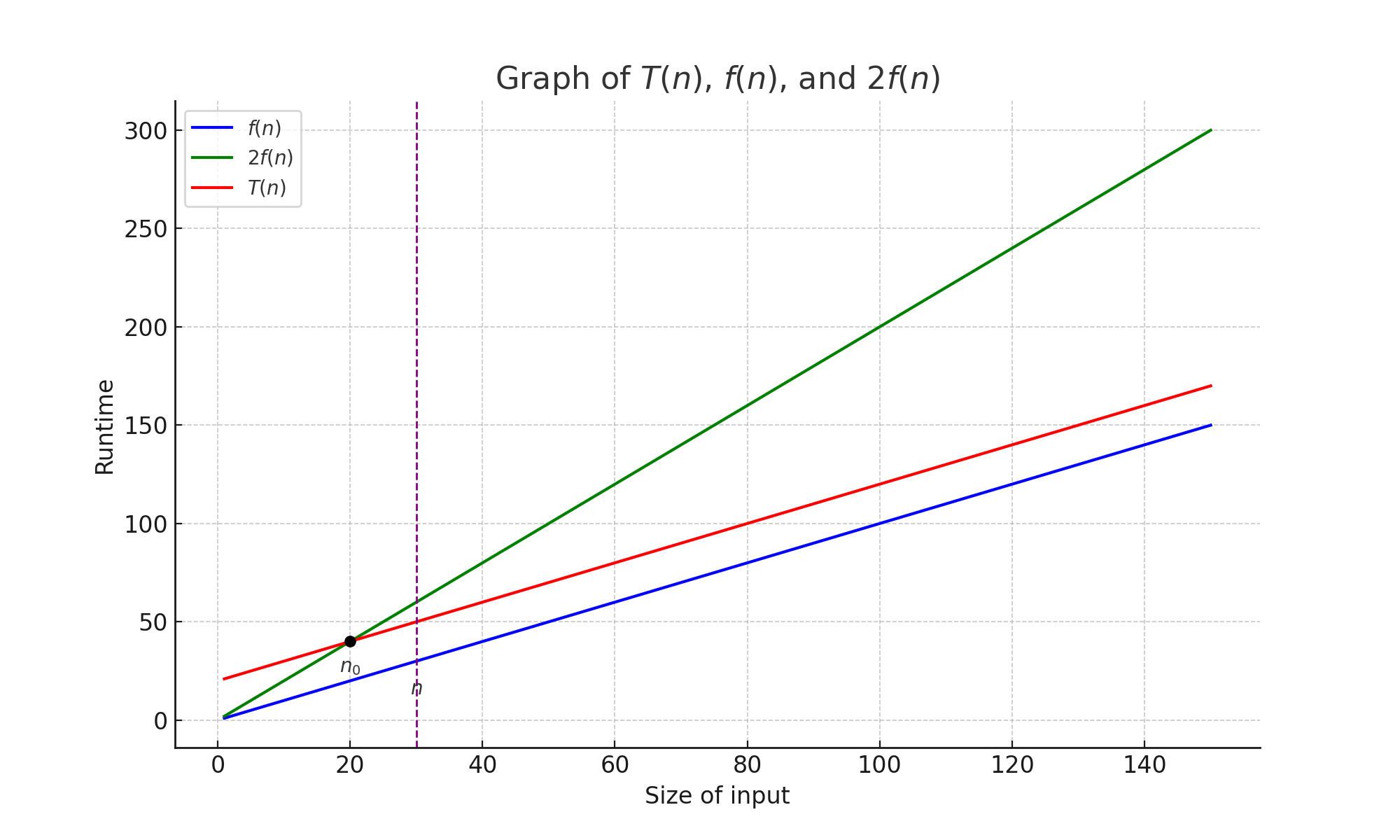
$$ f(n) = O(g(n)) \text{ if there exist constants } c > 0 \text{ and } n_0 > 0 \text{ such that } 0 \leq f(n) \leq c \cdot g(n) \text{ for all } n \geq n_0. $$

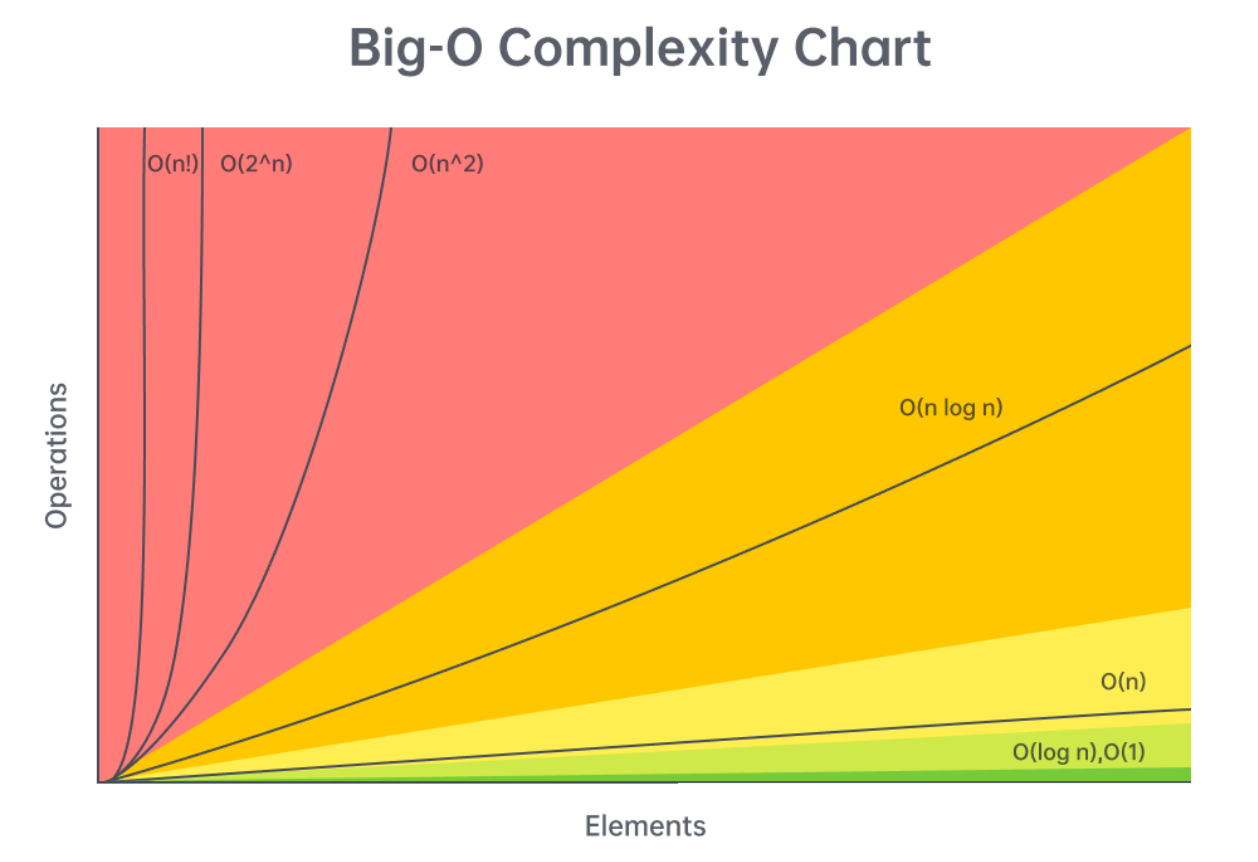
Characterstics
- Constants are ignored: $1000n = O(n)$
- Low-order terms are ignored: $n^3 + n^2 + n = O(n^3)$
It is essential to consider constants sincne Big-O represents an upper bound on the growth rate of an algorithm's complexity.

Consider:

$$ T(n) = n \log n $$ $$ U(n) = 50 n $$
- $T(n) = U(n) \text{ if } n = 2^{50}$
  - If $n$ is small ($< 2^{50}$) $ \Rightarrow U(n) \text{ grows more slowly than } T(n)$
  - If $n$ is large ($> 2^{50}$) $ \Rightarrow T(n) \text{ grows more slowly than } U(n)$
- In the case, $U(n)$ might be preferred since $n$ is more likely to be $< 2^{50}$

Big-O Classifications

$O(1)$: Constant
- The algorithm does NOT depend on the input size.
$O(\log n)$: Logarithmic
- The algorithm gets slightly slower as $n$ grows.
$O(n)$: Linear
- The runtime grows as much as $n$ grows (When $n$ doubles, runtime doubles).
$O(n \log n)$: Linearithmic
- Usually the result of performing $O(\log n)$ operation $n$ times or performing $O(n)$ operation $\log n$ times.
$O(n^2)$: Quadratic
$O(2^n)$: Exponential
$O(n!)$: Factorial

Data Structures

General-Purpose Data Structures
- Arrays
- Linked Lists
- Hash Tables
- Binary Search Trees
Special-Purpose Data Structures (Abstract Data Types (ADTs))
- Stack (LIFO)
- Queue (FIFO)
- Priority Queues
Sorting and Searching
- Linear Search and Binary Search
- Bubble Sort
- Selection Sort
- Insertion Sort
- Quick Sort
- Merge Sort
- Heap Sort
Graphs

Relationship of General-Purpose Data Structures

Back to Home Next Lecture