10. Recursion

Characteristics

1. Self-referential Functionality: A recursive function is distinguished by its ability to call itself, enabling the function to operate on smaller subsets of the problem.

2. Base Case: This acts as a termination criterion, preventing infinite recursion and ensuring that each recursive call progresses toward this condition.

3. Bookkeeping Overhead: Recursive calls involve considerable management of function states and return addresses, which can lead to increased memory usage.

Iterative/Recursive Comparison

/**
 * Sums from 1 to n iteratively.
 * @param n, positive integer
 * @return sum from 1 to n
 */
public static int sum(int n) {
    int result = 0;
    for (int i = 1; i <= n; i++) {
        result = result + i;
    }
    return result;
}

/**
 * Sums from 1 to n recursively.
 *
 * recSum(5)                               15
 *    5+recSum(4)                     10+5=15
 *      4+recSum(3)               6+4=10
 *        3+recSum(2)         3+3=6
 *          2+recSum(1) = 1+2=3
 * @param n
 * @return sum from 1 to n
 */
public static int recSum(int n) {
    if (n == 1) {
        return n;               // base case
    }
    return n + recSum(n - 1); // recursive case
}

Fibonacci Numbers

/**
 * Finds n-th fibonacci number.
 * @param n, positive value or 0
 * @return n-th fibonacci number
 */
public static long fib(int n) {
    if (n == 0 || n == 1) {
        return n;
    }
    return fib(n - 1) + fib(n - 2);
}

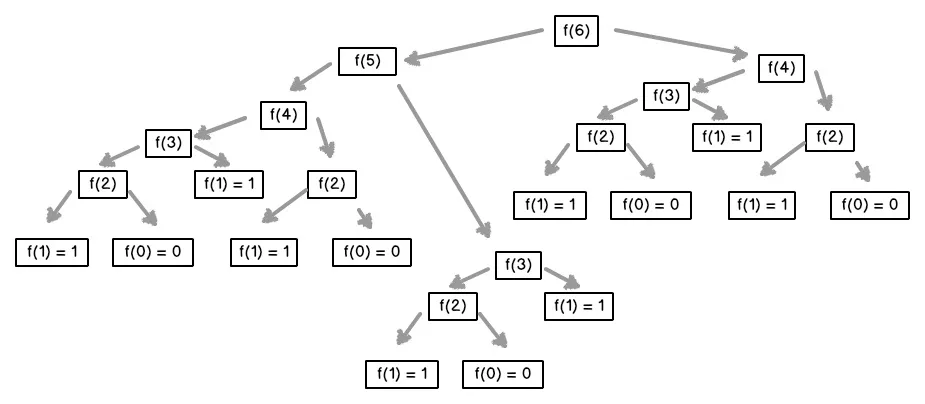
Recursion Tree for fib(6):

Binary Search (Recursive)

/**
 * Binary search in a non-null array.
 * @param data, int array to search against (ordered in ascending order)
 * @param key, int key value to search for
 * @return index if found, -1 if not found
 */
public static int find(int[] data, int key) {
    return find(data, key, 0, data.length - 1);
}

/**
 * Private helper method for binary search that uses recursion.
 * @param data, int array to search against (ordered in ascending order)
 * @param key, int key value to search for
 * @param lowerBound, lower bound index of the array
 * @param upperBound, upper bound index of the array
 * @return index if found, -1 if not found
 */
private static int find(int[] data, int key, int lowerBound, int upperBound) {
    // Base case 1: not found
    if (lowerBound > upperBound) {
        return -1;
    }

    int mid = lowerBound + (upperBound - lowerBound) / 2;

    // Base case 2: found
    if (data[mid] == key) {
        return mid;
    }

    // Recursive cases
    if (data[mid] < key) {
        return find(data, key, mid + 1, upperBound);
    }
    return find(data, key, lowerBound, mid - 1);
}

Back to Home Next Lecture