4. ArrayList and Binary Search

Java ArrayList

java.util.ArrayList

Methods

• add(E e)

• add(int index, E e)

• set(int index, E e)

• get(int index)

• remove(int index)

• size()

• addAll(Collection<? extends E> c)

• addAll(int index, Collection<? extends E> c)

• clone(): Returns a shallow copy of the ArrayList instance

• indexOf(Object o)

• isEmpty()

• removeIf(Predicate<? super E> filter)

Characteristics

• ArrayList in Java is created by default with a capacity of $10$

  • Can be initialized with a capacity of $0$

• ArrayList will expand when add() is called, but DOES NOT shrink when remove()

  • Programmers should manually invoke void trimToSize() method (shrink size to No. elements) to free up the memory

Dynamically Change Length

• ArrayList used to implement the Doubling-up Policy

• In Java 6: $(\text{oldCapacity} * 3) / 2 + 1$

  • Add $1$ to ensure at least some increase for corner cases: $\text{oldCapacity} \in {0, 1}$

  /**
   * Appends the specified element to the end of this list.
   * @param e element to be appended to this list
   * @return <tt>true</tt> (as specified by {@link Collection#add})
   */
  public boolean add(E e) {
      ensureCapacity(size + 1); // Increments modCount
      elementData[size++] = e;
      return true;
  }
  
  /**
   * Increases the capacity of this ArrayList instance, if necessary, to ensure that it can hold
   * at least the number of elements specified by the minimum capacity argument.
   * @param minCapacity the desired minimum capacity
   */
  public void ensureCapacity(int minCapacity) {
      modCount++;
      int oldCapacity = elementData.length;
      if (minCapacity > oldCapacity) {
          int newCapacity = (oldCapacity * 3)/2 + 1;
          if (newCapacity < minCapacity)
              newCapacity = minCapacity;
          elementData = Arrays.copyOf(elementData, newCapacity);
      } 
  }
  

Amortized Analysis

Runtime Complexity Analysis of add(E e) Method

List<Integer> numbers = new ArrayList<Integer>(4);

Assuming doubling up the array

Use banker’s (accounting) method to show Amortized Analysis

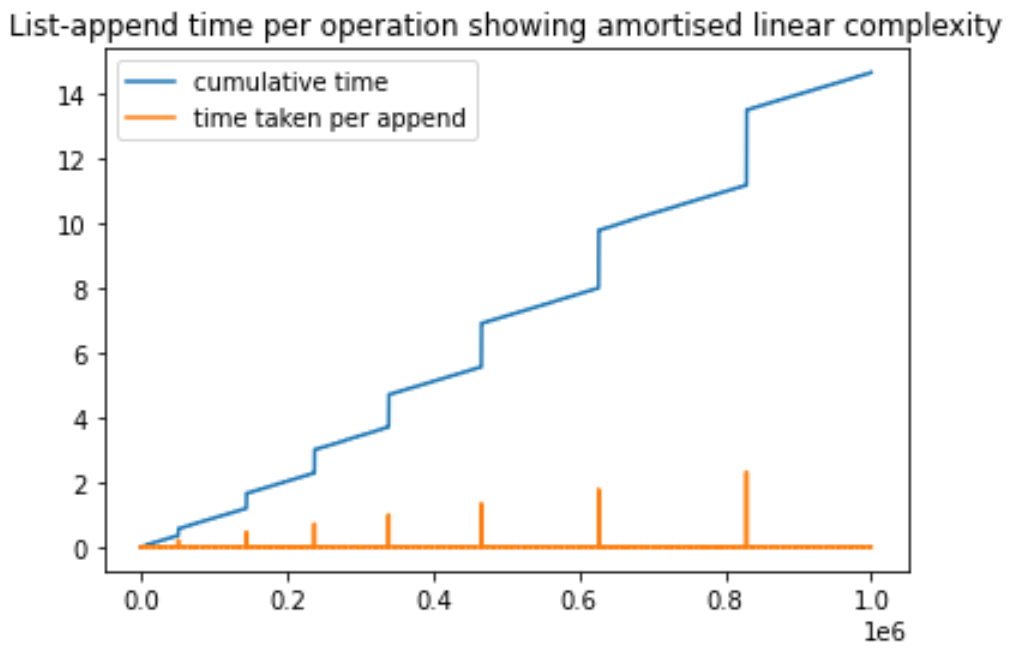
Conclude that add(E e) method has amortized constant time due to the allocated dollars per operation

Latency Issue of Amortized Constant Time

Binary Search

Prerequisite: The array is sorted.

public static int binarySearch(int[] data, int key) {
    int l = 0;
    int r = data.length - 1;
    int mid;

    while (true) {
        if (l > r) {
            return -1;
        }

        mid = l + (r - l) / 2; // Not mid = (l + r)/2
        
        if (data[mid] == key) {
            return mid;
        }

        if (data[mid] < key) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
}

Time Complexity

Binary Search: $O(\log n)$

• In general, $\lfloor \log_{2} n \rfloor+ 1$ operations to split an array in half before it is empty.

• The base of $\log$ does not significantly impact the complexity class: $$c * \log_{10}(x) = \log_2(x) \text{ where } c = \frac{\log (10)}{\log (2)} = 3.3219 $$

• $O(\log n)$ does NOT grow proportionally with the input size $n$ but only increases by a constant factor. $$ c \cdot \log_2(2 * n) = c \cdot (\log_2 2 + \log_2 n) = c + c \cdot \log_2 n $$

Integer Overflow

Avoid potential integer overflow issue with mid = l + (r - l) / 2

• Ones' Complement of a binary number is the value obtained by flipping all the bits in the binary representation of the number.

• Most Significant Bit (MSB) is known as the sign bit, used to represent whether the number is positive (0) or negative (1).

• Twos' Complement, the negative equivalent of the original binary number, is get by:

  1. Taking Ones' Complement
  2. Adding 1

  Bits	Unsigned value	Signed value (Two's complement)	One's Complement	Two's Complement
  000	0	0	111	000
  001	1	-1	110	111
  010	2	-2	101	110
  011	3	-3	100	101
  100	4	-4	011	100
  101	5	3	010	011
  110	6	2	001	010
  111	7	1	000	001

• With $n$ bits, we can represent unsigned numbers of range: $$[0, 2^{(n-1)}]$$

• With $n$ bits, we can represent signed numbers of range: $$[–2^{(n-1)}, 2^{(n-1)}–1]$$

Array & ArrayList

1. Random access
2. No holes allowed -> Shifts
3. Immutable length -> Memory/Latency issue

Back to Home Next Lecture